Author: Yiming Ma, Yao Zeng, and Anthony Lee Zhang, The University of Chicago

Compiled by: Qian Jiayan

Stablecoins are a type of crypto asset designed to be pegged to the US dollar, but are backed by dollar-denominated assets that are not perfectly liquid. We find that there is a phenomenon of concentrated arbitrage in stablecoins: the largest issuer, Tether, allows an average of only six institutions to redeem stablecoins for cash each month. This paper argues that the issuer's choice of concentrated arbitrage reflects a trade-off: efficient arbitrage helps improve the price stability of stablecoins in the secondary market, but it amplifies the risk of runs by reducing the price impact of investors selling stablecoins. The findings of this paper suggest that policies aimed at improving the price stability of stablecoins may have the unintended consequence of increasing the risk of stablecoin runs. The Financial Technology Research Institute of Renmin University of China (WeChat ID: ruc_fintech) has compiled the core parts of the research.

I. Introduction

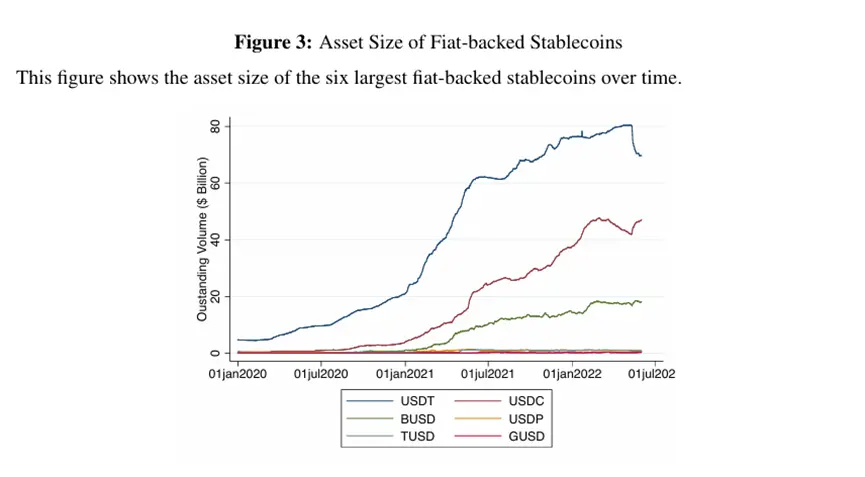
Fiat-backed stablecoins are blockchain assets that claim to maintain a stable value of 1 US dollar. This price stability is achieved by committing to back each stablecoin token with at least 1 dollar's worth of dollar-denominated assets (such as bank deposits, government bonds, corporate bonds, and loans). The market capitalization of the six major fiat-backed stablecoins has grown from $5.6 billion at the beginning of 2020 to over $130 billion at the beginning of 2022. Stablecoins have the potential to become a widely accepted means of payment, competing with fiat currencies and bank deposits, which has sparked active discussions about how to mitigate potential risks to financial stability and what the optimal regulatory framework should be.

An ideal stablecoin would always trade at a stable 1 dollar and would not experience panic runs. However, stablecoins hold illiquid assets while promising a fixed redemption value of 1 dollar. Unlike money market funds (MMFs) or commercial banks, this 1 dollar redemption is limited to specific institutional arbitrageurs. The vast majority of investors can only trade stablecoins on secondary markets, similar to how investors trade ETF shares in secondary markets. These investors trade at secondary market prices, which often fluctuate around 1 dollar due to supply and demand pressures in the market. Given that the price of stablecoins is determined in equilibrium, when and why would stablecoin investors want to redeem? What is the relationship between the price deviation of stablecoins and their run risk?

This paper answers these questions by constructing a framework of the stablecoin market structure, demonstrating how issuers, arbitrageurs, and customers interact to determine the stability of stablecoin prices and the likelihood of panic runs. The findings of this paper provide important insights for the optimal regulation of stablecoins. These insights are particularly relevant as different jurisdictions have recently proposed various regulatory schemes for stablecoins, which are not always consistent with one another.

First, some proposals require stablecoin issuers to offer unrestricted direct redemptions to all investors, effectively eliminating the current two-tier market structure. Such policies would indeed promote price stability through more competitive arbitrage. However, in cases where stablecoins are allowed to continue liquidity conversion, our model suggests that more efficient arbitrage would also amplify the risk of panic runs. In contrast, imposing redemption fees on arbitrageurs would reduce run risk by limiting arbitrage, but at the cost of sacrificing price stability.

Second, many policy proposals impose restrictions on the safety and liquidity of the reserve assets held by stablecoin issuers. Our findings suggest that reserve asset policies should be coordinated with policies managing redemptions, as these factors jointly determine the outcomes of price stability and run risk.

Third, allowing the payment of dividends further enhances the price stability of stablecoins and may reduce run risk. In summary, while price stability and low run risk are both ideal characteristics of stablecoins, they are inherently different and respond differently to policy interventions.

II. Detailed Description of Stablecoins

Stablecoins are blockchain assets that claim to maintain a stable value of 1 US dollar. Blockchain assets can be self-custodied: users can directly hold, send, and receive stablecoins using cryptocurrency wallet software such as MetaMask. These stablecoins are not held in any trusted intermediary: instead, a "private key" (a long numerical code typically stored only on the user's hardware device) is used to prove ownership of the stablecoins to the blockchain network and instruct the network to take actions such as transferring stablecoins to other wallets. Others cannot access an individual's private key, so they cannot withdraw funds from the individual's wallet.

Compared to other blockchain assets like Bitcoin, a significant feature of stablecoins is their relative price stability. The largest stablecoin issuers attempt to achieve price stability by committing to back each stablecoin token with at least 1 dollar's worth of off-chain dollar assets. These fiat-backed stablecoins have experienced rapid expansion in recent years. Within two years, the total asset size of the six major fiat-pegged stablecoins grew from $5.6 billion at the beginning of 2020 to over $130 billion at the beginning of 2022 (Figure 3). The two largest stablecoins are Tether (USDT) and Circle's USD Coin (USDC), which reached a combined market capitalization of $76.4 billion in January 2022, accounting for over 50% of the total market size. The sizes of Binance USD (BUSD), Paxos (PUSD), TrueUSD (TUSD), and Gemini Dollar (GUSD) are much smaller.

In the remainder of this section, we outline the uses of stablecoins and the market structure of stablecoins.

2.1 Uses of Stablecoins

Stablecoins provide a relatively low-cost way to transact and hold dollar-denominated assets. If a remitter in Country A sends money to a recipient in Country B, she can purchase stablecoins with the fiat currency of Country A on a cryptocurrency exchange, withdraw these stablecoins to her cryptocurrency wallet, and then send them to the wallet of the recipient in Country B. The recipient can then deposit these funds into a local cryptocurrency exchange, convert the stablecoins into fiat currency, and withdraw the fiat currency. Sending stablecoins from one cryptocurrency wallet to another is relatively quick and low-cost. As of January 2023, transactions involving sending stablecoins on the Ethereum blockchain can be completed within a minute, with each transaction costing about 1 dollar, regardless of the amount of stablecoins sent. Stablecoins can also serve as a means of storing value; they can be held in cryptocurrency wallets indefinitely for free.

Thus, while the cost of using stablecoins is higher than well-functioning banking services in developed countries, they are competitive in situations where traditional financial infrastructure is lacking. For example, stablecoins are widely used in environments where transactions must cross borders, capital controls and financial repression are prevalent, inflation rates are high, or trust in financial intermediaries is low.

Stablecoins are also used for trading with other blockchain smart contracts. For instance, market participants can use stablecoin tokens to purchase other blockchain tokens, such as ETH, MKR, or UNI, through automated market maker protocols like Uniswap. Market participants can also lend stablecoin tokens on lending protocols like Aave and Maker to earn positive interest rates, or use these assets as collateral to borrow other assets. To some extent, stablecoins provide a secure means of storing value and a medium of exchange for the blockchain ecosystem.

2.2 Market Structure

Stablecoin tokens are created (or "minted") in the primary market in the form of cash in US dollars and redeemed (or "burned"), as shown on the left side of Figure 4. To create stablecoin tokens, arbitrageurs send 1 dollar to the issuer, and the issuer sends one stablecoin token to the market participant's cryptocurrency wallet. Similarly, to redeem stablecoin tokens, market participants send one stablecoin token to the issuer's cryptocurrency wallet, and the issuer sends 1 dollar to the market participant's bank account via bank transfer. The primary market for stablecoins is similar to money market funds in the traditional financial system.

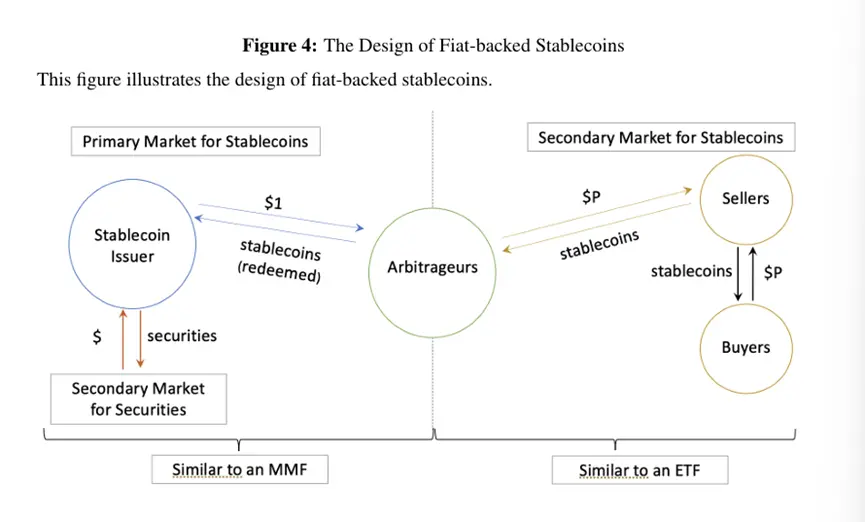
Most market participants cannot become arbitrageurs to redeem and create stablecoin tokens, and there are differences in the ease and cost of market participants entering the primary market based on the stablecoin issuer. According to market participants, USDC allows general businesses to register as arbitrageurs, while USDT requires a lengthy due diligence process and imposes restrictions on the registration location of arbitrageurs. Additionally, USDT has a minimum trading size of $100,000 and charges a fee of 0.1% or the greater of $1,000 for each redemption.

Most market participants exchange existing stablecoins for fiat currency in the secondary market. Cryptocurrency exchanges allow investors to deposit US dollars and then trade between dollars and stablecoins with other market participants. Therefore, the price of stablecoin tokens in the secondary market is determined by supply and demand. When there is a surge in stablecoin sell-offs, the price in the secondary market drops, but this does not directly lead to the liquidation of reserve assets. In this way, buying and selling stablecoins in the secondary market is similar to trading ETF shares in a competitive exchange.

However, the sell-off pressure in the secondary market may spread to the primary market through arbitrageurs. When the price in the secondary market falls below 1 dollar, arbitrageurs can profit by purchasing stablecoin tokens in the secondary market and redeeming them with the stablecoin issuer at a 1:1 ratio for 1 dollar in the primary market. Through this arbitrage, the redemption value of stablecoins in the primary market at 1 dollar pulls the trading price of stablecoins in the secondary market toward 1 dollar. At the same time, this arbitrage process also means that when the stablecoin issuer liquidates reserves to meet cash redemptions from arbitrageurs, the sell-off pressure from secondary market investors will ultimately trigger the sale of reserve assets. If illiquid reserve assets are sold at a discount, the costs of these sell-offs can be particularly high.

III. Data

In this section, we will explain our main data sources.

Primary Market Data:

The core dataset used in this analysis consists of data on each stablecoin creation and redemption event for the six largest fiat-backed stablecoins (USDT, USDC, USDP, TUSD, and GUSD) on the Ethereum, Avalanche, and Tron blockchains. We obtained this data from the "block explorers" of each blockchain, which process transaction-level blockchain data into usable formats. This paper uses Etherscan for Ethereum data, Snowtrace for Avalanche data, and Tronscan for Tron data. Through the data extraction process, we can see the exact timestamps of each stablecoin creation and redemption event, the number of stablecoins redeemed or created, and the wallet addresses of the entities involved in the stablecoin creation and redemption. The blockchain only records wallet addresses, and the same institution may have multiple wallet addresses. During the data collection process, this paper merges wallet addresses that are clearly labeled as belonging to the same institution on Etherscan. However, this process may not be exhaustive, so the calculated concentration of arbitrage should be viewed as a lower bound of the true concentration of arbitrage.

Secondary Market Data:

For each stablecoin, this paper extracts the hourly closing prices of direct USD-to-stablecoin trades from several major exchanges, including Binance, Bitfinex, Bitstamp, Bittrex, Gemini, Kraken, Coinbase, Alterdice, Bequant, and Cexio. The differences in stablecoin prices among major exchanges are generally negligible, so the price series is not significantly affected by the weights assigned to different exchanges. This paper applies a 1% winsorization to the secondary market prices.

IV. Other Facts about Stablecoins

In this section, this paper presents a set of new facts about stablecoins to provide a basis for the model and calibration.

4.1 Secondary Market Prices

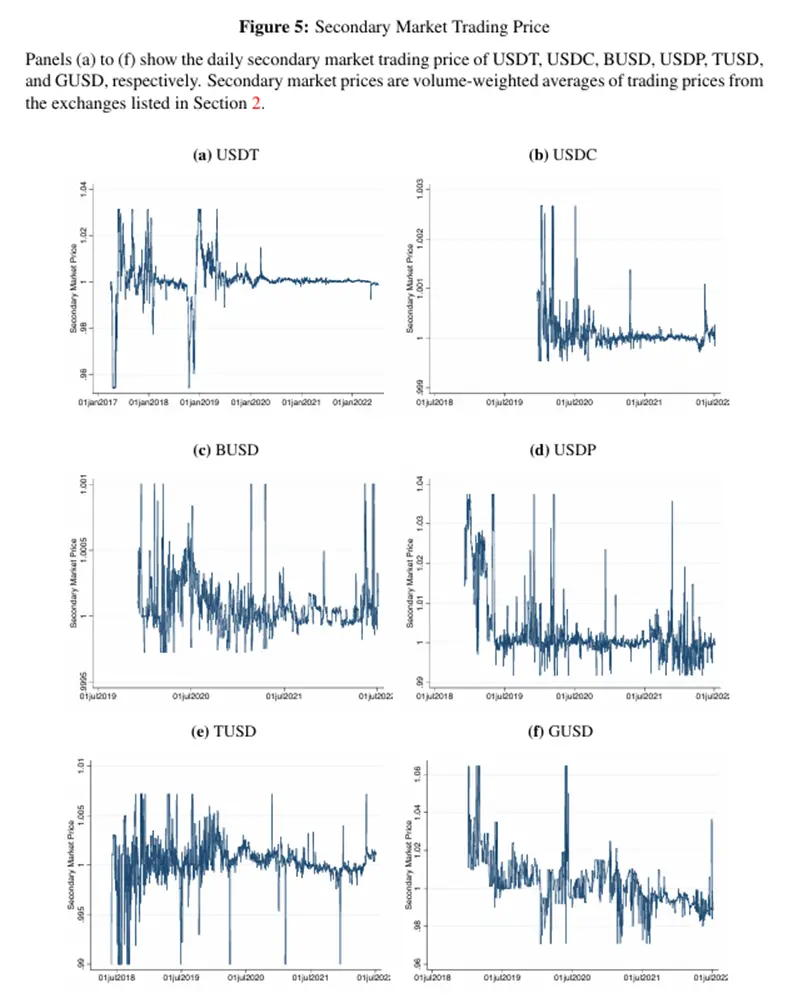
Fact 1: The trading prices of stablecoins in the secondary market often deviate from 1 dollar.

Figure 5 shows the trading prices of different stablecoins in the secondary market over time. This paper observes that secondary market prices rarely fixate at 1 dollar. Instead, among the sample of stablecoins, they trade at a discount 27.2% to 41.6% of the time and at a premium 57.3% to 72.8% of the time (see Table 1a). The extent of these price deviations varies by stablecoin. While USDT has an average discount of 54 basis points, USDC has an average discount of only 1 basis point. The average discounts for BUSD, TUSD, and USDP are also lower than that of USDT, while GUSD has the highest average discount. The magnitude of the median discount is generally smaller than the average discount, but the cross-sectional differences remain similar. For example, the median discount for USDT is 11 basis points, while the median discount for USDC is less than 1 basis point. When considering a common sample period, the magnitude also decreases.

Starting from January 2020, when all six stablecoins were trading, differences among the coins still existed, with USDT having a greater average discount than USDC (see Table 1b). The average premiums and median premiums also show significant differences across the cross-section.

4.2 Primary Market Concentration

Fact 2: The redemption and creation of stablecoins in the primary market are executed by a small number of arbitrageurs, with varying degrees of concentration depending on the stablecoin.

Table 2 shows the characteristics of monthly primary market redemption and creation activities for different stablecoins on the Ethereum blockchain. On average, USDT has only 6 arbitrageurs participating in redemptions each month, while USDC has 521. The concentration of market share among arbitrageurs is generally high but varies by stablecoin. The largest arbitrageur of USDT accounts for 66% of all redemption activities, while the largest arbitrageur of USDC accounts for 45%. In contrast, most other stablecoins have a number of arbitrageurs and concentration levels that fall between those of USDT and USDC. In terms of trading volume, the average monthly redemption amount for USDT is $577 million, while for USDC, it is $2.976 billion. In comparison, the total outstanding tokens for USDT are 1.5 to 2 times that of USDC. Therefore, the larger number of USDC arbitrageurs and lower concentration is also related to the relatively high redemption volume in relation to total asset size. The creation volume is larger, and the number of arbitrageurs participating in creation is relatively high, but the trends and arbitrage concentration remain similar across different stablecoins.

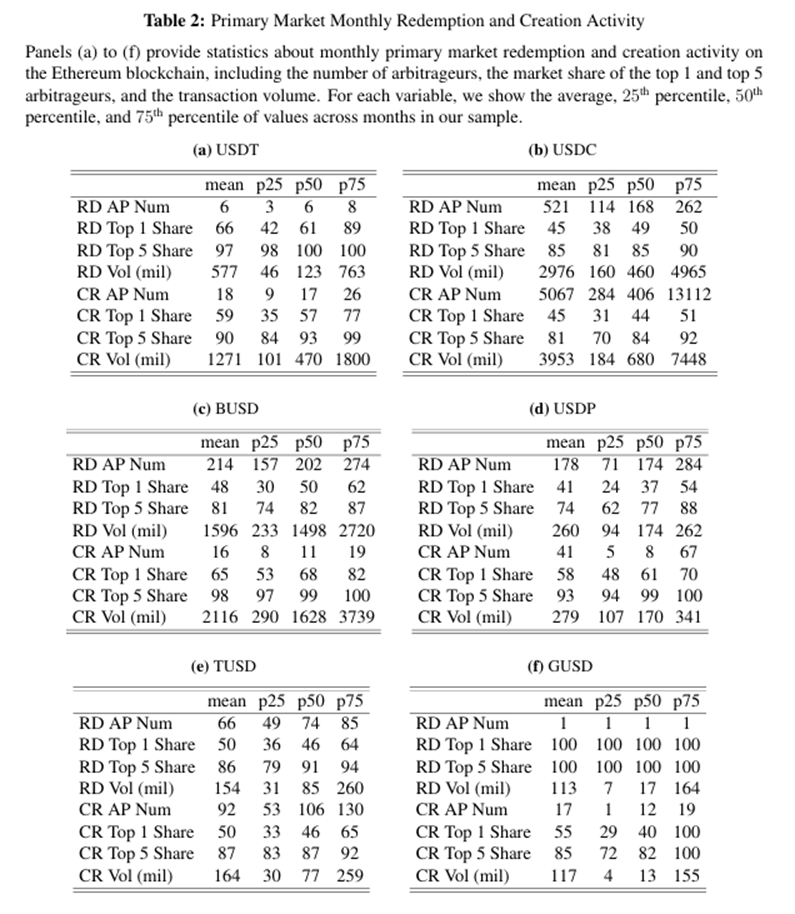
4.3 Secondary Market Prices and Primary Market Concentration

Fact 3: Stablecoins with a more concentrated group of arbitrageurs exhibit more pronounced price deviations in the secondary market.

Next, we analyze the relationship between price deviations and arbitrageur concentration. For a given stablecoin, the monthly secondary market price deviation is calculated by averaging the absolute value of daily price deviations from 1 over a given month, including deviations above and below 1. We then average the monthly data to obtain the average price deviation for that stablecoin. Similarly, we count the number of unique arbitrageurs participating in redemptions and/or creations and calculate the market share of the top five arbitrageurs for each stablecoin over time.

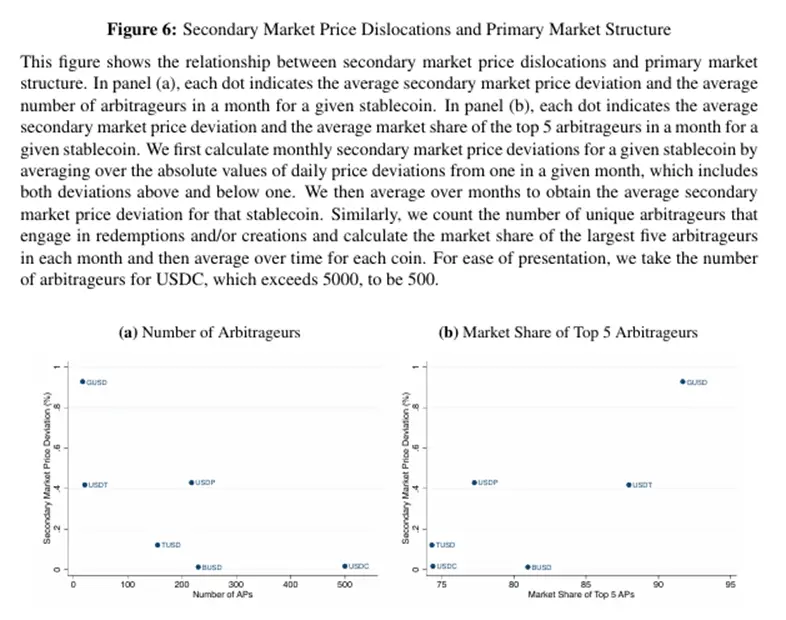
The results are shown in Figure 6a. A clear negative trend emerges: stablecoins with more arbitrageurs (like USDC) have a higher average price deviation from 1 compared to stablecoins with fewer arbitrageurs (like USDT). Another measure of arbitrageur concentration is through the market share of the largest arbitrageur. In Figure 6b, we repeat the analysis using the market share of the top five arbitrageurs. This relationship is positively correlated. Stablecoins where the top five arbitrageurs consistently hold a large share of total redemptions and creations have a higher average price deviation than other stablecoins with lower arbitrageur concentration. In other words, it seems that higher arbitrage competition is associated with a reduction in secondary market price misalignment.

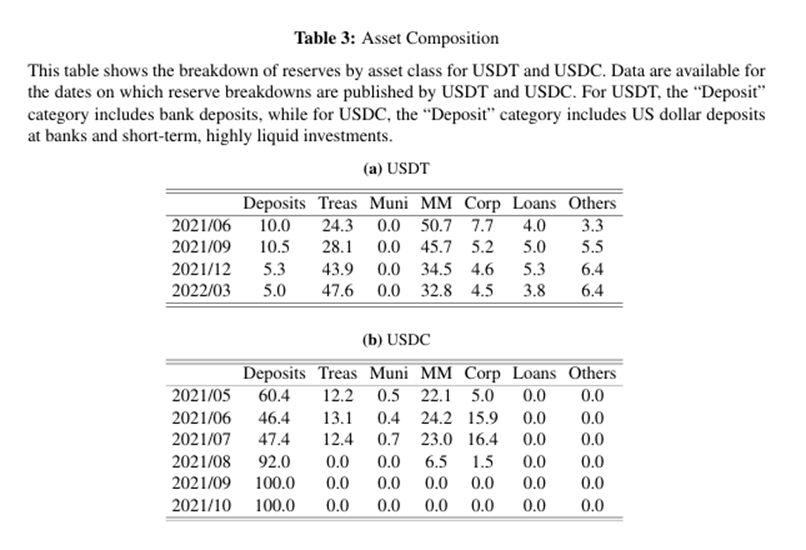
4.4 Liquidity Conversion

Fact 4: Stablecoins undergo varying degrees of liquidity conversion by investing in illiquid assets.

Stablecoin issuers hold dollar-denominated assets of varying degrees of illiquidity as reserves. Table 3 shows the composition of the reserves for USDT and USDC as of the reporting date. Overall, the reserve assets of both USDT and USDC are not fully liquid, with USDT's reserve assets being more illiquid.

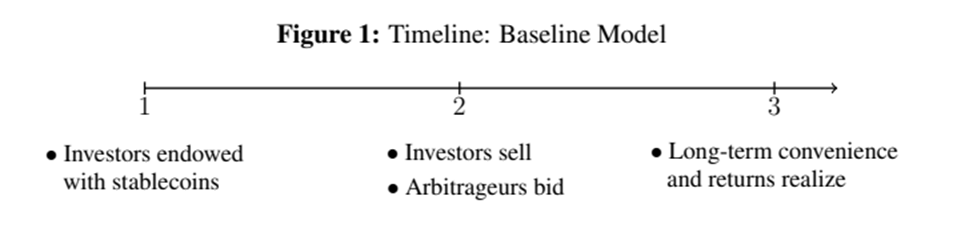
V. Theoretical Framework

5.1 Centralization of Stablecoin Runs and Arbitrage

The benchmark economic model is built on the research of Diamond and Dybvig (1983) and consists of three time points, t = 1, 2, 3, with no time discounting. This paper provides a timeline in Figure 1 to illustrate this economic model:

There are two groups of risk-neutral participants:

1) A group of stablecoin investors indexed by i, and

2) A group of n stablecoin arbitrageurs.

There are two types of assets:

1) US dollars, which are risk-free and highly liquid, used as the unit of account;

2) An illiquid and potentially productive reserve asset.

Investors collectively hold stablecoins initially backed by reserve assets at t = 1. The initial value of the reserve assets is normalized to 1 dollar. At t = 2 and t = 3, investors must decide whether to redeem their stablecoins early at t = 2 (which may trigger a run) or hold until t = 3 to obtain long-term returns (which we will detail below). Unlike bank depositors, stablecoin investors cannot directly redeem their held stablecoins from the issuer. Instead, at t = 2, they sell stablecoins to arbitrageurs in the secondary market according to the mechanism proposed by Jacklin (1987) and Farhi, Golosov, and Tsyvinski (2009), and then the arbitrageurs redeem cash from the issuer. Like these models, investors sell stablecoins by independently submitting market orders. This assumption is consistent with empirical evidence indicating that retail investors are more likely to use market orders, especially when spreads are narrow (Kelly and Taitelbaum, 2013), which is the case for stablecoins. This paper uses λ to denote the proportion of investors selling stablecoins at market price p2.

Arbitrageurs compete in a double auction to determine the price p2 at which investors sell λ stablecoins, considering the amount they expect to redeem from the issuer. In the benchmark model, it is assumed that arbitrageurs cannot hold net inventories, so their net redemption amount in the primary market at t = 2 must equal their purchase amount in the secondary market. In Appendix C.1, we show that this assumption is consistent with the empirical observation that the number of stablecoins held by the vast majority of arbitrageurs is very small. Arbitrageurs face secondary inventory costs: arbitrageur j incurs costs to arbitrage zj units of stablecoins from the secondary market to the primary market, where χ can be viewed as a measure of the arbitrageur's balance sheet capacity: when χ is high, inventory costs are low.

When deciding whether to redeem their stablecoins early, investors receive private information about the economic fundamentals at t = 3 at t = 2. Following the global game literature, each investor i receives a private signal θi = θ + εi at t = 2, where the noise term εi is independently and uniformly distributed over [-ε, ε]. This paper focuses on arbitrarily small noise, i.e., ε → 0, but the model results also hold outside the limit case.

The fundamental θ reflects the overall risk level and determines the long-term value of the stablecoin at t = 3. With a probability of 1 - π(θ), the economy enters a bad state: the reserve assets fail, and investors receive neither nominal returns nor any long-term benefits from holding stablecoins backed by worthless assets. With a probability of π(θ), the economy enters a good state: the reserve assets generate a positive value R(ϕ) ≥ 1 dollar, owned by the issuer. The stablecoin continues to operate, and the remaining 1 - λ investors receive long-term returns η > 0 per stablecoin, with each unit of remaining reserve assets receiving the initial value of 1. This long-term return η can be explained by the returns investors earn from lending out stablecoins.

Using backward induction, we first consider p2, the price received by investors when they redeem stablecoins early. In the main text, we derive the inverse demand function generated by competitive bidding from arbitrageurs. If arbitrageurs engage in strategic bidding, the model in this paper is similar to the setting of Klempere and Meyer (1989), which has multiple equilibria. However, under the equilibrium selection rule that chooses the equilibrium bidding curve closest to the standard linear solution, the core economic insight of this paper regarding the impact of arbitrage capacity on stablecoin prices remains unchanged.

This paper derives the inverse demand function by setting the price equal to the marginal cost.

Assuming λ ≤ 1−ϕ, which means the issuer is solvent, then arbitrageurs purchasing zj units at price p2 in the secondary market and redeeming in the primary market will obtain:

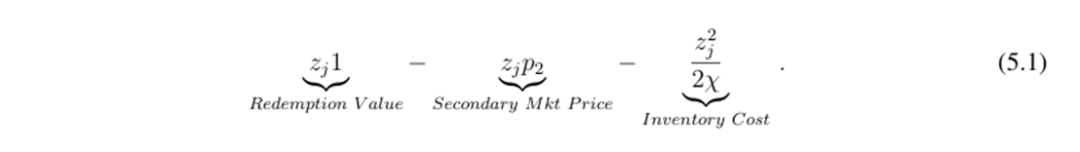
In any symmetric equilibrium, the total inventory absorbed by each arbitrageur is z∗ j = λ n. If the issuer takes the price as given, in order for z∗ j to be the optimal quantity absorbed, the price must equal the marginal value of absorbing an additional quantity of stablecoins at z∗ j. That is, by differentiating (5.1) with respect to zj, setting it equal to 0, and then solving for p2, we obtain:

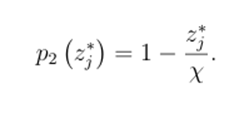
In words, the price is the marginal redemption value of 1 minus the marginal inventory cost z∗ j χ. Substituting z∗ j = λ n into the symmetric equilibrium gives:

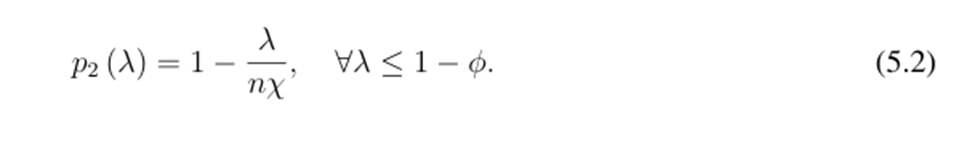
In the case of insolvency, λ > 1 - ϕ, each unit of the stablecoin can only be redeemed at its liquidation value (1 - ϕ)/λ. Since investors submit market orders, the redemption value does not depend on the number of arbitrageurs. Therefore, the profits of the arbitrageurs are adjusted to:

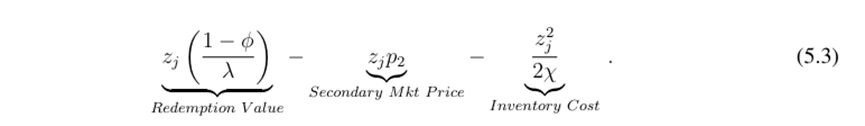
Similarly, in symmetric equilibrium, the price must equal the marginal value of arbitrageurs absorbing additional quantities. By differentiating (5.3) with respect to zj, setting it equal to 0, and substituting zj∗ = λn, we obtain:

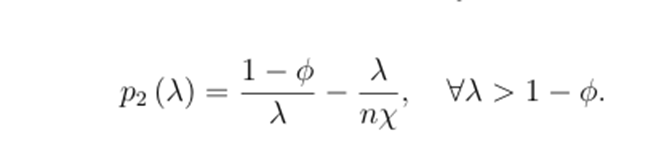
The only difference from (5.2) is that the redemption value is modified to (1−ϕ)/λ. This paper summarizes these results in the following lemma.

Lemma 1. The secondary market price of the stablecoin at t = 2 is given by:

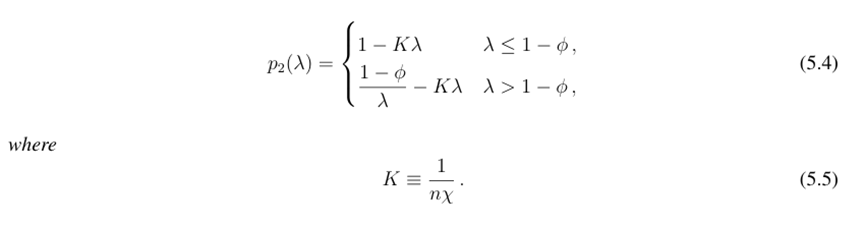
Lemma 1 indicates that for any total redemption amount λ > 0, p2 decreases with an increase in K and increases with an increase in χ and n. Intuitively, when arbitrageurs are in a better capital position (higher χ) and in greater numbers (higher n), the secondary market price is less affected by investor sell-offs. We refer to K as arbitrage capacity, which plays a central role in the analysis as it measures the slope of secondary market demand when the issuer remains solvent. The bids from arbitrageurs create a downward-sloping demand curve for the stablecoin, and as n or χ increases, the slope becomes steeper, thereby reducing the price impact of stablecoin sell-offs.

It is also important to note that p2 strictly decreases with λ everywhere: the more investors sell off, the lower the price. This is significant because it creates strategic substitutability in investors' sell-off decisions: when many other investors are selling, a particular investor expects the proceeds from their sell-off to decrease, thereby suppressing their selling behavior. This force contrasts with the strategic complementarity found in classic bank run models (such as Diamond and Dybvig, 1983), where depositors can withdraw a fixed value of their deposits.

Next, this paper examines the situation at t = 3.

The global game framework can solve for a unique equilibrium for any fundamental parameter value. Theoretically, we can obtain:

Proposition 1: There exists a unique threshold equilibrium in which investors sell stablecoins if the signal they receive is below the threshold θ∗, and do not sell otherwise.

Proposition 1 indicates that the model with private and noisy signals for investors has a unique threshold equilibrium. The liquidation decision of investors is uniquely determined by their signals: they will only sell stablecoins at t = 2 if their signal is below a certain threshold. In other words, when the signal is at the threshold, there is indifference between selling and holding. Given the existence of a unique run threshold, we can prove that the indifference condition implies the following Laplace equation:

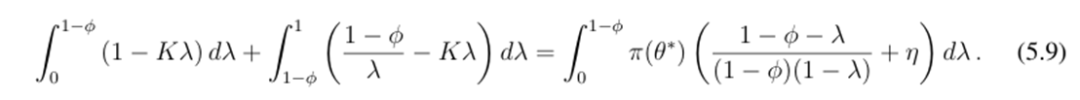
Solving the Laplace equation yields an analytical solution for the run threshold and presents an intuitive comparative static analysis regarding the risk of stablecoin runs:

Proposition 2: The run threshold is given by:

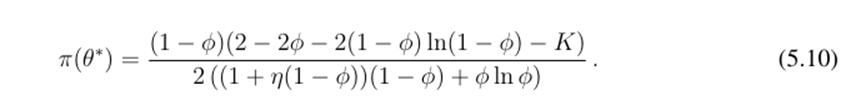
i). The run threshold, or run risk, decreases with an increase in K (i.e., increases with an increase in n and increases with an increase in χ).

ii). The run threshold, or run risk, increases if and only if ϕ increases.

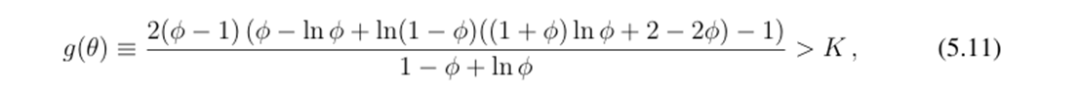
Where g(ϕ) is continuous and strictly decreasing in ϕ, and satisfies limϕ→0 g(ϕ) > 0.

A core theoretical result is the first part of Proposition 2, which indicates that more effective arbitrage, i.e., a smaller K value, exacerbates run risk.

The second part of Proposition 2 indicates that when g(ϕ) > K, the higher the level of liquidity conversion of the stablecoin, the higher the run risk. For a given K, this condition holds when ϕ is sufficiently small. Intuitively, when stablecoins hold more illiquid reserve assets, the first-mover advantage among investors increases, as those investors who choose not to sell will have to involuntarily bear higher liquidation costs triggered by selling investors.

5.2 Price Stability and Optimal Stablecoin Design

After analyzing the run risk of stablecoins and its relationship with arbitrage concentration, we extend the benchmark model by incorporating the price stability of stablecoins at t = 1 and the optimal design choices of the issuer in the pre-trade game at t = 0.

The specific reasoning process is detailed in the original text. Regarding the optimal choice of arbitrageur concentration by stablecoin issuers, we derive the following result:

Proposition 3: Assume G is linear, and ϕ is sufficiently small such that (5.11) holds, then the issuer's optimal choice of K decreases with ϕ: if the liquidity of reserve assets is poorer, the issuer will optimally choose a more concentrated arbitrage sector.

Proposition 3 stems from the trade-off between price stability and financial stability. Stablecoin issuers choose the arbitrage concentration K to balance the benefits of reducing run risk against the costs of reducing price stability. When asset illiquidity ϕ is high, run risk increases. At this point, issuers should be more willing to sacrifice price stability to limit run risk, leading to a higher optimal value of K.

VI. Policy Implications

Multiple jurisdictions have given more attention to the optimal regulation of stablecoins. Regulators and market participants desire stablecoins to have both low run risk and maintain price stability. The framework of this paper emphasizes that these two ideal goals are distinct and driven by different economic forces. In particular, we highlight the trade-off between price stability and financial stability and indicate that some policies may achieve one goal at the expense of the other. In this section, we use model predictions to elucidate what proposed regulations on stablecoin redemptions, reserves, and interest payments mean for price stability and financial stability.

Through a series of analyses, this paper finds that dividend issuance may have other effects. For example, dividend issuance may intensify price competition among stablecoin issuers, which could encourage new entrants and improve allocation efficiency. Under U.S. securities law, stablecoins that issue dividends may also be classified as securities and face regulatory risks. We will leave the analysis of these and other factors for future research.

VII. Conclusion

This paper analyzes the trade-off between stablecoin run risk and price stability. From a macro perspective, stablecoin runs stem from liquidity conversion. Stablecoin issuers hold illiquid assets while providing arbitrageurs with the option to redeem stablecoins at a fixed 1 dollar in the primary market. This liquidity mismatch propagates from the primary market, potentially triggering runs by secondary market investors even with exchange trading.

Importantly, the run risk of stablecoins is moderated by the market structure of the arbitrageur sector, which acts as a "firewall" between the secondary and primary markets. When the arbitrageur sector is more efficient, shocks in the secondary market are transmitted more effectively to the primary market. Consequently, the price stability of stablecoins improves, but the first-mover advantage for sellers also increases, thereby raising run risk. If the arbitrageur sector is less efficient, the transmission of shocks from the secondary market will be poorer. Price stability will be affected, but run risk will decrease, as the price impact of stablecoin trading in the secondary market will suppress panic selling by market participants.

The findings of this paper have significant policy implications. Although both regulators and market participants desire stablecoins to have low run risk and maintain price stability, these two ideal goals are distinct and driven by different economic forces. In particular, allowing unrestricted redemptions will enhance arbitrage efficiency, which, while helping to improve price stability, may come at the cost of higher run risk. When discussing whether stablecoins should be allowed to distribute profits to investors in the form of dividends, the suppressive effect of dividend issuance on run risk must also be considered. Overall, when designing regulatory measures, it is crucial to simultaneously consider price stability and run risk for the future sound operation and safety of the stablecoin industry.

免责声明：本文章仅代表作者个人观点，不代表本平台的立场和观点。本文章仅供信息分享，不构成对任何人的任何投资建议。用户与作者之间的任何争议，与本平台无关。如网页中刊载的文章或图片涉及侵权，请提供相关的权利证明和身份证明发送邮件到support@aicoin.com，本平台相关工作人员将会进行核查。