Original Author: Anastasia Matveeva, Co-founder of Gonka Protocol

In the previous article, we explored the fundamental contradiction between security and performance in decentralized reasoning with LLMs. Today, we will fulfill our promise and delve into a core issue: how do you truly verify that a node in an open network is running the exact model it claims to be, without any deception?

01. Why Verification is So Difficult

To understand the verification mechanism, it is helpful to review the internal process of a Transformer during inference. When input tokens are processed, the last layer of the model produces logits—i.e., the raw, unnormalized scores for each token in the vocabulary. These logits are then transformed into probabilities through the softmax function, forming a probability distribution over all possible next tokens. At each generation step, a token is sampled from this distribution to continue generating the sequence.

Before diving into potential attack vectors and specific verification implementations, we first need to understand why verification itself is difficult.

The root of the problem lies in the non-determinism of GPUs. Even with the same model and input, different hardware, or even the same device, may produce slightly different outputs due to issues like floating-point precision.

The non-determinism of GPUs makes it meaningless to directly compare output token sequences. Therefore, we need to examine the internal computation process of the Transformer. A natural choice is to compare the output layer, specifically whether the probability distributions over the model's vocabulary are close. To ensure we are comparing the probability distributions of the same sequence, our verification program requires the verifier to fully reproduce the exact token sequence generated by the executor, and then compare these probability distributions step by step. This process will produce a verification proof to demonstrate the model's authenticity.

However, the probabilistic nature also brings a subtle balance: we need to punish persistent cheaters while avoiding mistakenly penalizing honest nodes that simply had bad luck and produced low-probability outputs. If the threshold is set too strict, we risk harming good actors; if set too lenient, we let bad actors slip through.

02. The Economics of Cheating: Gains and Risks

Potential Gains: The Temptation is Huge

The most direct attack is "model substitution." Suppose the network deployment requires a significant amount of computational power for the Qwen3-32B model; a rational node might think, "What if I secretly run the much smaller Qwen2.5-3B model and pocket the savings from the computational power difference?"

Using a 3 billion parameter model to impersonate a 32 billion parameter model could reduce computational costs by an order of magnitude. If you can deceive the verification system, it’s akin to receiving rewards for high computational power while delivering results from low-cost computation.

More cunning attackers might use quantization techniques, claiming to run at FP8 precision while actually using INT4 quantization. The performance difference may not be significant, but the cost savings are still considerable, and the outputs may be similar enough to pass simple verification.

At a more complex level, there are also pre-filling attacks. This type of attack allows the attacker to generate proofs for the outputs of a cheap model as if those outputs were generated by the complete model expected by the network. Here’s how it works:

For example, consensus is reached on-chain to deploy a Qwen3-235B model with a specific parameter set.

1. The executor generates a sequence using Qwen2.5-3B: `[Hello, world, how, are, you]`.

2. The executor computes the proof for Qwen3-235B for these identical tokens through a single forward pass: `[{Hello: 0.9, Hi: 0.05, Hey: 0.05}, …]`.

3. The executor submits the probabilities of Qwen3-235B as proof, claiming that the inference came from Qwen3-235B.

In this case, the probabilities come from the correct model, making them appear legitimate, but the actual sequence generation process is much cheaper. Since the complete model could theoretically generate the same outputs as the smaller model, the results may seem entirely legitimate from a verification standpoint.

Potential Losses: The Costs are Higher

While deceiving the system may yield considerable gains, the potential losses are equally significant. The real challenge for cheaters is not passing a single verification but rather evading detection long-term and systematically, ensuring that their computational "discounts" outweigh the penalties the network might impose.

In the Gonka network, we designed a sophisticated economic deterrent mechanism:

• Everyone is a verifier: Each node verifies a portion of the network's reasoning according to its weight.
• Reputation system: New nodes start with a reputation of 0, and all reasoning is verified. With continued honest participation, reputation grows, and verification frequency can drop to 1%.
• Penalty mechanism: If caught cheating, reputation resets to zero, requiring about 30 days to rebuild.
• Epoch settlement: In an epoch lasting about 24 hours, if caught cheating a statistically significant number of times, all rewards for that epoch are forfeited.

This means that a cheater trying to save 50% on computational power could end up losing 100% of their gains. This "lose-lose" risk makes cheating economically unviable. The problem we aim to solve with the verification mechanism is not to catch every suspicious inference but to draw a clear line ensuring we can continuously catch fraudsters with a high probability while not harming the reputation of honest participants.

03. How to Catch Cheaters? Three Verification Solutions

So, how do we catch these attacks? This question can be divided into two parts: 1) Is the distribution in the verification proof close to the distribution produced by the claimed model? 2) Is the output text indeed generated based on the submitted proof?

Solution One: Probability Distribution Comparison (Core Foundation)

When the executor generates inference output (e.g., `[Hello, world, how, are, you]`), they record a verification proof that includes the final output and the top K probabilities for each position in the output sequence (e.g., for the first position, it is `[{Hello: 0.9, Hi: 0.05, Hey: 0.05}, …]`, etc.). The verifier then forces its model to follow the exact same token sequence and calculates the normalized distance of probabilities at each position \( d_i \):

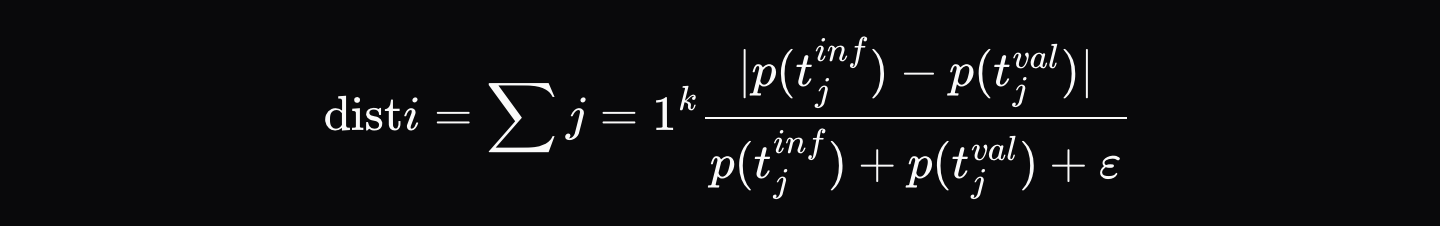
Where \( p_{\text{artifact},ij} \) is the probability of the j-th most likely token at that position in the inference proof, and \( p_{\text{validator},ij} \) is the probability of the same token in the verifier's distribution.

The final distance metric is the average sum of distances for each token:

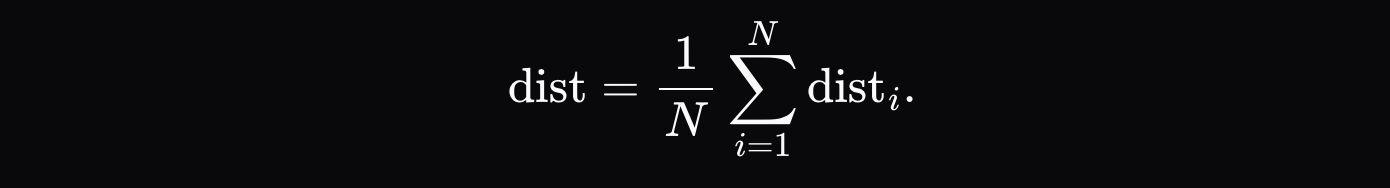
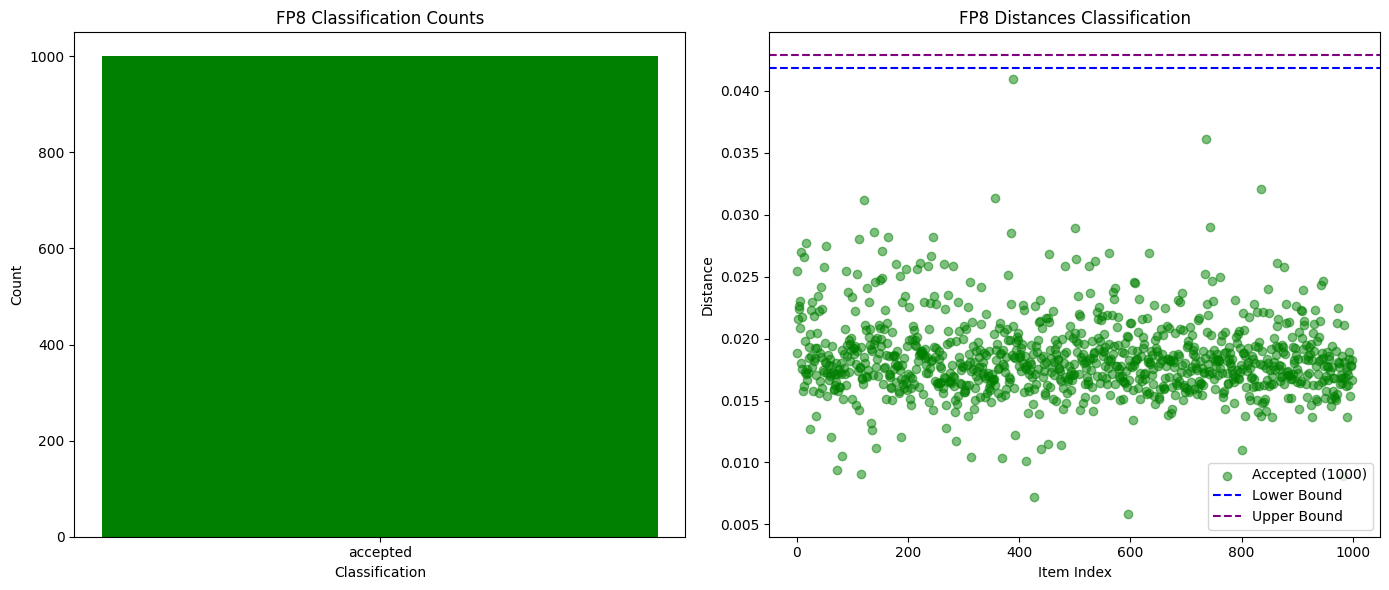
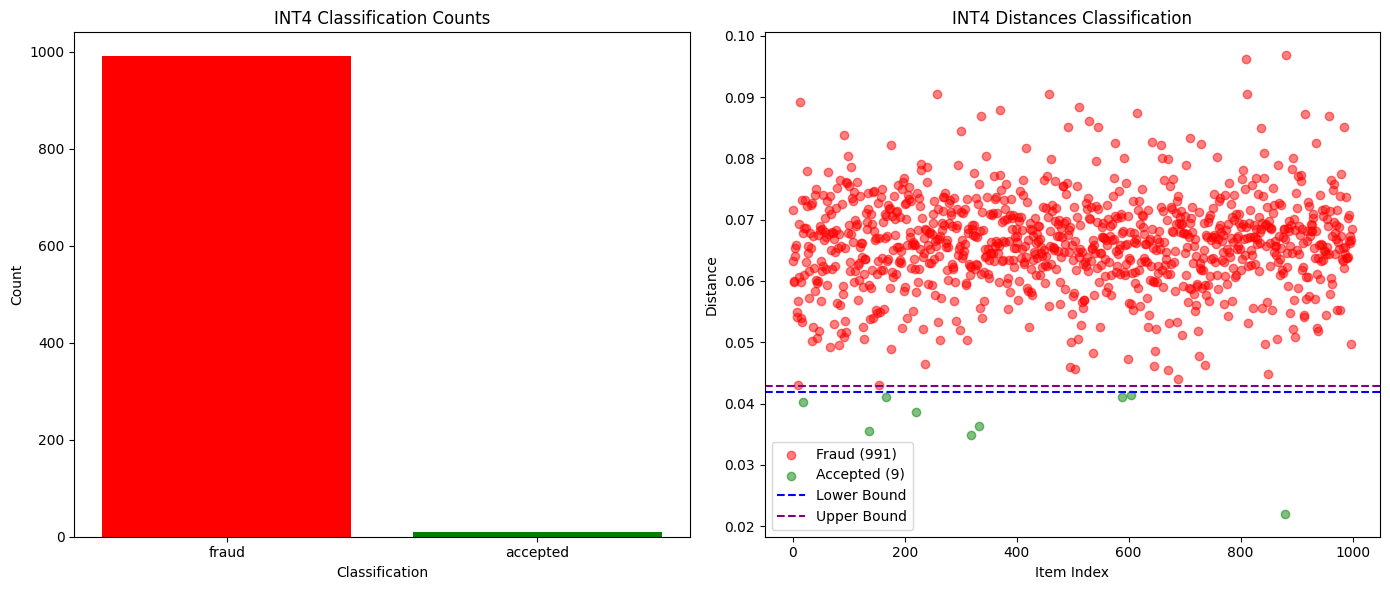
For capturing completely different models, or even different quantized versions of the same model, comparing the top K probabilities has proven sufficient. As shown in the chart below, when we tested between Qwen3-32B FP8 and INT4 quantized versions, we achieved a 99% fraud detection rate with zero false positives. The differences in probability distributions of other models are also significant enough to easily detect cheating within an epoch, while honest participants remain safe.

The following chart compares the successful and failed verification counts between Qwen3-32B FP8 (honest) and INT4 quantization (fraud):

The following chart shows the change in probability distribution distance for Qwen3-32B FP8 (honest) vs INT4 quantization (fraud) as sequence length varies:

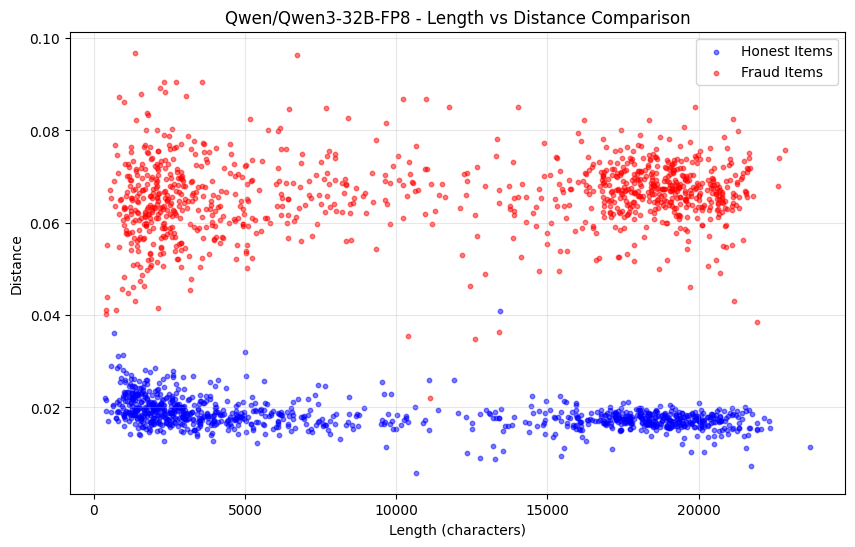
However, the drawback of relying solely on this method is that it cannot guard against pre-filling attacks. If the probabilities do match the distribution of the complete model, but the sequence was generated by a smaller model, we have several additional methods to capture this situation.

Solution Two: Perplexity Detection (Defense Against Pre-filling Attacks)

In addition to verifying whether the proof comes from the correct model, we also check whether the output text is "likely" to have come from the probability distribution of that proof.

If the sequence is generated by a different model, its perplexity relative to the claimed model's probability distribution will be abnormally high. In tests, we distinguished between Qwen2.5-7B and Qwen2.5-3B pre-filling attacks, with significant differences in perplexity.

The most intuitive way to capture pre-filling attacks is to check perplexity: in addition to verifying whether the proof was generated by the claimed model, we can also check whether the output text is likely to have been generated from the submitted distribution:

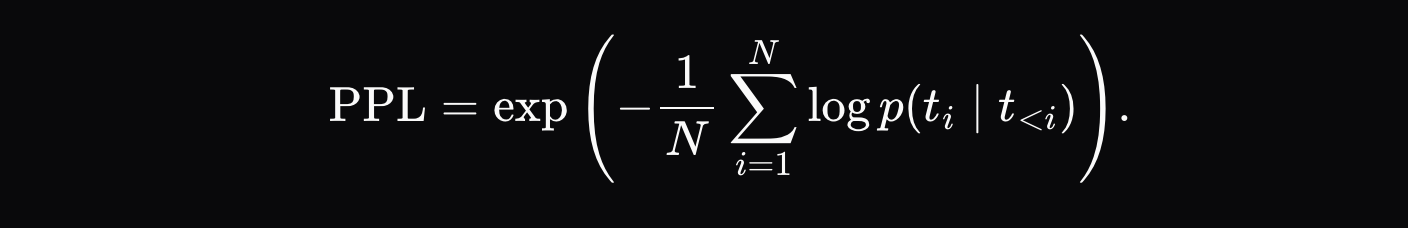
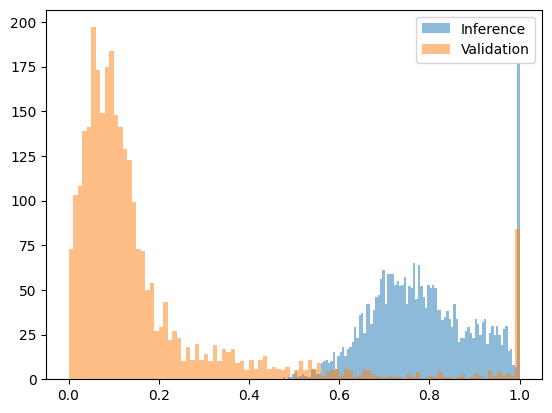
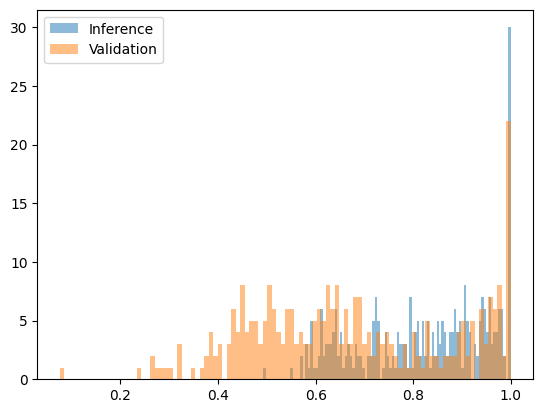
If the perplexity is too high, it indicates that the sequence was likely generated by a different model. This method works well for defending against attacks using significantly different models. When we tested sequences generated by Qwen2.5-3B but claimed to come from Qwen2.5-7B, the difference in perplexity was clear enough to set a distinct threshold. The following chart shows a transformed perplexity function fitted to the interval [0, 1], where the output of the 7B model mostly falls below 0.2, while the outputs of the pre-filling attack (3B model outputs paired with 7B model probabilities) all fall above 0.4.

The following chart shows the transformed perplexity function for Qwen2.5-7B (honest) vs Qwen2.5-3B pre-filling attack (fraud):

However, perplexity detection has limitations compared to similar models and different quantized versions of the same model. For example, comparing the w8a16 and w8a8 quantized versions of Qwen2.5-7B did not show significant differences.

The following chart shows the transformed perplexity function for Qwen2.5-7B w8a16 (honest) vs w8a8 quantization (fraud):

Fortunately, attacking using similar models is usually economically unviable. If they run a model that costs 70-90% of the claimed model, plus perform a scoring calculation on the real model, the computational resources they actually spend may be more than simply running the real model honestly.

It is important to note that a single low-probability output generated by honest participants will not significantly lower their reputation. If such low-probability outputs do not occur consistently for that participant, meaning it is merely a random statistical outlier, they will still receive the full reward at the end of the epoch.

Solution Three: RNG Seed Binding (Deterministic Solution)

This is the most thorough solution: binding the output sequence to a random number generator seed.

The executor uses a deterministic seed derived from the request (e.g., `run_seed = SHA256(user_seed || inference_id_from_chain)`) to initialize the RNG. The verification proof includes this seed and the probability distribution.

The verifier uses the same seed for verification: if the sequence indeed comes from the probability distribution of the claimed model, the same output must be reproducible. This provides a deterministic "yes/no" answer, completely eliminating pre-filling attacks, and the verification cost is much lower than full inference.

04. Outlook: The Future of Decentralized AI

We share these practices and thoughts out of a firm belief in the future of decentralized AI. As AI models increasingly permeate social life, the demand to bind model outputs to specific parameters will only grow stronger.

The verification solution chosen by the Gonka network has proven feasible in practice, and its components can be reused in other scenarios that require verification of AI inference authenticity.

Decentralized AI is not only a technological evolution but also a transformation of production relations—it seeks to solve the most fundamental trust issues in an open environment through algorithms and economic mechanisms. The road ahead is long, but we have taken a solid step forward.

Original link

免责声明：本文章仅代表作者个人观点，不代表本平台的立场和观点。本文章仅供信息分享，不构成对任何人的任何投资建议。用户与作者之间的任何争议，与本平台无关。如网页中刊载的文章或图片涉及侵权，请提供相关的权利证明和身份证明发送邮件到support@aicoin.com，本平台相关工作人员将会进行核查。