Author: Gryphsis Academy
The prediction market Polymarket is not a "gambling site that plays with probabilities." Understanding the pricing logic is essential to finding arbitrage opportunities. In the context of financial engineering, it actually represents a combination of three roles:
An information aggregator (including insider trading)
A structured derivatives exchange
A pricing engine that transforms "whether something will happen in the future" into "something that can be traded today"
What it does is compress human judgments about the future into a tradable number in real-time. To truly understand Polymarket's asset pricing system, we cannot merely stop at the level of "YES sells for 0.63, indicating a 63% probability."
We need to start from first principles:
Probability Theory → Financial Engineering → No-Arbitrage Pricing → Order Book Structure → Risk-Neutral Probability, from which we seek arbitrage opportunities.
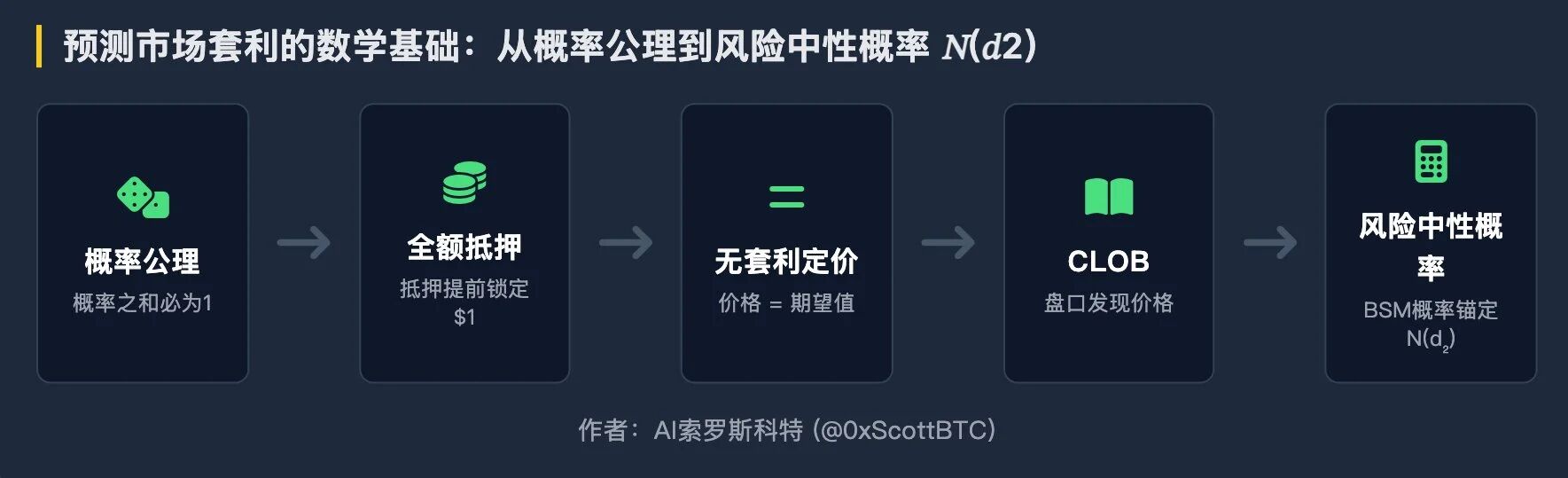
1. Basics of Probability Theory — Events, Sample Space, and Constraints
Any question of "whether something will happen in the future" is mathematically a problem of probability theory. Let's dive into the first lesson of probability theory.
1. Sample Space (Sample Space, denoted as Ω): This is "the complete set of all possible outcomes for this future event." The requirements are:
Exhaustive: All possible outcomes are listed.
Mutually Exclusive: Two outcomes cannot be true at the same time.
In the most common binary market on Polymarket, for example:
Will the closing price of Bitcoin be above $150,000 on December 31?
This market can be abstracted as: Ω = {Yes, No}
In other words, at the time of settlement, only "Yes" or "No" can occur.
2. Event (Event, denoted as (E)): An event is a subset of the sample space. In this example:
EY = {Yes}
EN = {No}
We assign a probability measure P(.) to the event.
According to Kolmogorov's probability axioms, the following must hold:
Non-negativity: P(E) ≥ 0
Normalization: P(Ω) = 1
Additivity (for mutually exclusive events): P(EY U EN) = P(EY) + P(EN)
Since EY U EN = Ω, we immediately get: P(Yes) + P(No) = P(Ω) = 1
This means:
The mathematical hard constraint: the sum of these two probabilities must equal 1.
This conclusion seems simple, but it is the anchor point for all subsequent pricing derivations. Any quote claiming "this event has an 80% chance of occurring while the other side has a 30% chance" is mathematically contradictory and inevitably allows for arbitrage. This is very important: Any prediction market like Polymarket is primarily a probability measure space; this is a problem of probability structure.

2. Basics of Financial Engineering — How $1 is Guaranteed to be Redeemed
Mathematics gives us "probabilities must add up to 1," and the next question is: how does the market turn this into "money"?
The core design of Polymarket is Full Collateralization. It locks in "the winner takes $1" using structured collateral, avoiding the old problem of "someone wins but no one pays."
The mechanism works as follows:
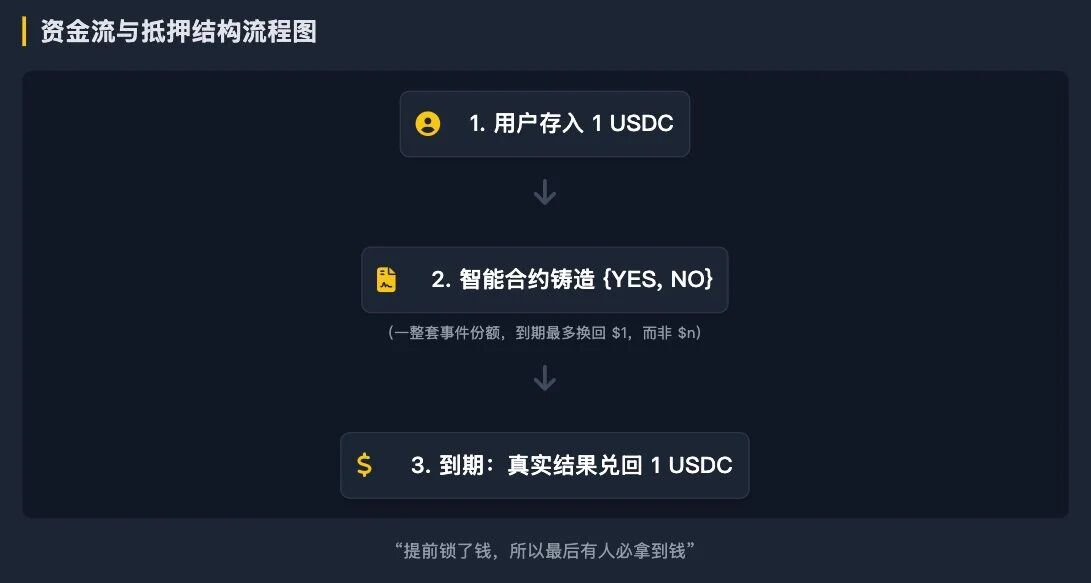
1. Minting: Participants deposit collateral into the contract, typically 1 USDC.
2. Receiving "a complete set of outcome shares": In return, the contract immediately mints and issues a complete set of "outcome tokens" covering all possible outcomes in this market.
For a binary market: 1 USDC → 1 YES-Token + 1 NO-Token
For a market with (n) possible outcomes: 1 USDC → (n) tokens, each representing one specific outcome (Outcome A, Outcome B, …).
A very critical point:
Although you receive one of each outcome, due to the mutual exclusivity of all events, only "the token of the outcome that actually occurs" can be redeemed for 1 USDC, while other outcomes become zero.
Thus, at maturity, this entire set of shares can redeem at most $1, not $n.
In other words, the system locks in sufficient funds from Day 0 to ensure future redemption.
3. Settlement/Redeeming: When the event is determined by the oracle to be "Yes":
YES-Token holders can redeem the locked 1 USDC in the contract.
NO-Token becomes 0.
If the result is "No," then the reverse applies.
Therefore, structurally speaking, at the moment of final settlement of the event, a combination of {YES, NO} must be able to exchange for exactly $1.
Now let's discuss what this means for pricing.
Assume at a certain moment (before the event is settled), the two tokens in the market are priced as follows:
Price of YES-Token: V(Yes) dollars
Price of NO-Token: V(No) dollars
Consider the following two extreme cases:
If V(Yes) + V(No) = $0.98: A trader can spend $0.98 to buy one YES and one NO in the open market.
Regardless of whether the final result is Yes or No, at the time of settlement, these two can be redeemed for $1.
This means they have locked in the right to "receive $1 at maturity" at a cost of $0.98. This is equivalent to a contract for "certain future redemption of $1," implying an implied yield to maturity of approximately (1−0.98)/0.98 ≈ 2.04%.If V(Yes) + V(No) = $1.02: A market maker can deposit 1 USDC to mint a "complete set" {YES, NO}
and then immediately sell YES and NO in the market, cashing out $1.02.
They effectively use $1 of collateral to instantly get back $1.02, earning $0.02.
Notice the subtle differences between the two arbitrage scenarios:
The first (0.98 case) does not mean "immediate" access to $1, but rather "locking in a future redemption of $1," which requires holding until the event settles. This money is occupied during this period, equivalent to lending cash to the market, earning a risk-free discount return (provided the platform/oracle/USDC itself has no default risk).
The second (1.02 case) is instant risk-free arbitrage because it does not require waiting for maturity.

This tells us two things:
The structural design (full collateralization) ensures that the system can always redeem $1 at settlement, relying not on morality but on locked funds.
This structure imposes a very strong hard constraint pressure on pricing: V(Yes) + V(No) ≈ $1
We call this:
The anchoring relationship at the financial level: the sum of prices on both sides must be close to $1.
If we compare this with the probability constraint from the first part [P(Yes) + P(No) = 1], doesn't the form correspond?
3. Deriving from Expected Value to "Price = Probability"
Now we juxtapose the truths from the mathematical layer and the financial engineering layer:
Probability theory tells us: P(Yes) + P(No) = 1
Collateral structure + No-Arbitrage tells us: V(Yes) + V(No) ≈ $1
The shapes of these two equations are the same. This already hints at something very important: The price of YES essentially expresses "the probability of occurrence."
We can formalize this into a serious financial derivation.
Definition: Cash Flow of YES-Token
If the final result of the event is Yes: you receive $1.
If the result is No: you receive $0.
Thus, the future cash flow of buying a YES-Token is a simple two-point distribution. Its (undiscounted) expected value is: EV(YES) = P(Yes) × $1 + P(No) × $0 = P(Yes)
This means: in a rational, competitive, tradable market, the "fair value" of the YES-Token should equal its expected cash flow, i.e., P(Yes).
Furthermore, classic no-arbitrage logic tells us:
If the market price V(Yes) < EV(YES), i.e., price < fair value, traders will buy YES, driving up the price.
If V(Yes) > EV(YES), i.e., price > fair value, traders will sell YES (or equivalently buy NO), driving down the price.
The equilibrium point can only be: V(Yes) = EV(YES) ≈ P(Yes)
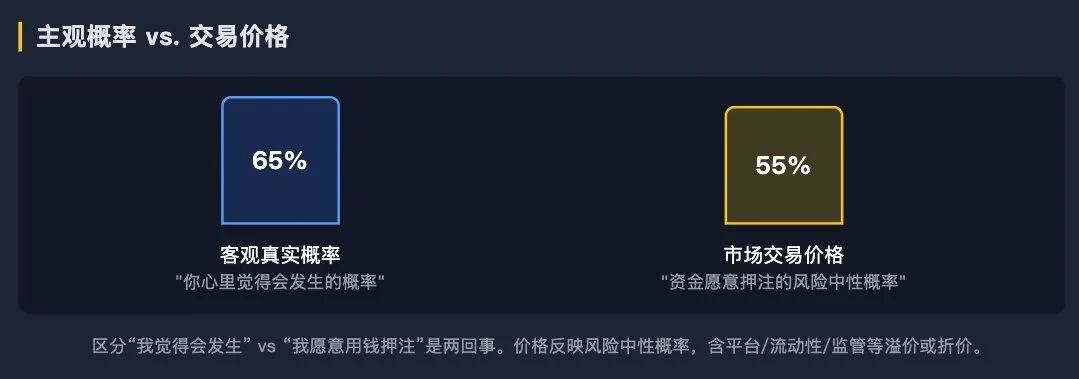
Thus, we conclude that price equals probability in prediction market products.
More strictly, the probability here is risk-neutral probability, not "the true probability from a god's perspective."
Why do we say this?
Because the real world has a risk premium.
If the event itself carries unhedgeable systemic risks (political, regulatory, black swan events, etc.), investors will demand additional compensation, leading to prices deviating from objective probabilities. Similarly, if the market is concerned about tail risks such as platform issues, oracle reliability, USDC custody, or regulatory crackdowns, the price of YES will be discounted.
In other words:
In an ideal world where everything is fully hedged, participants are risk-neutral, and capital constraints are loose:
V(Yes) = P(Yes)In the real world, a more precise statement is:
V(Yes) = Q(Yes) - (risk discount) + (liquidity/regulatory premium)
where Q(⋅) is the probability under the risk-neutral measure.
In layman's terms: the YES price of 0.63 on the screen represents "the probability estimate of this event occurring in a risk-neutral world, as assessed by those willing to bet real money in the market," adjusted for structural risk compensation.
This explains why for certain high-conflict, hard-to-hedge political events, Polymarket prices often do not align perfectly with polls (or even expert judgments). This is not the market being "wrong"; it is the market pricing in risk.
4. Pricing to Trading — From No-Arbitrage Formulas to CLOB Order Books
Up to this point, we have answered "why it has this price."
Now there are two more questions:
How is this price formed in the market?
How can I determine if it is "mispriced" and can be arbitraged?
Polymarket (especially after v3) uses a Central Limit Order Book (CLOB), no longer employing AMM constant function market making. This means the price is not calculated by a preset function but is "discovered" by the collective buy and sell orders of all participants.
We can break this part into two sub-layers: Execution Layer and Valuation Layer.
4.1 Execution Layer: Four Basic Actions in the Order Book
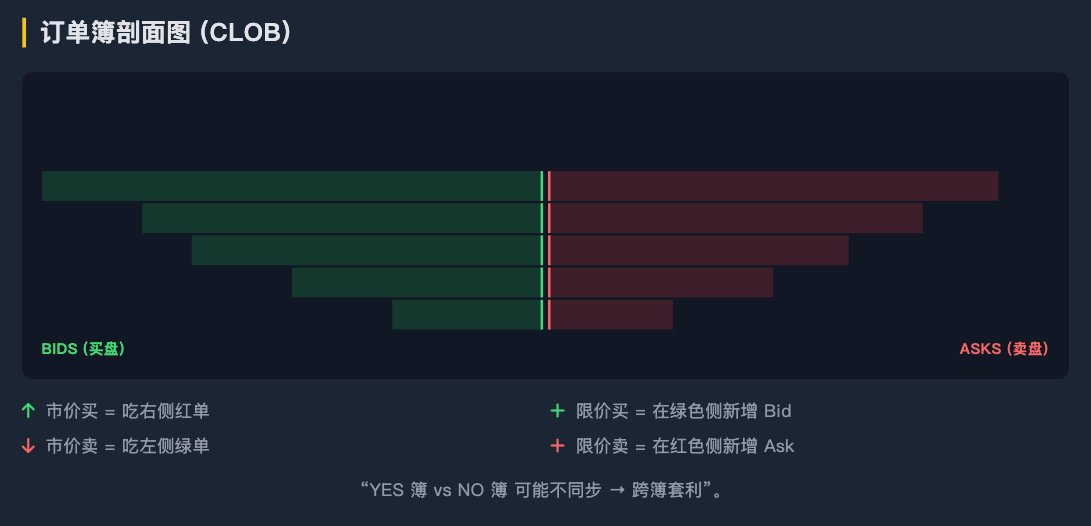
In the CLOB model, YES and NO each have independent order books. This is very important because it means that within a short time window, it is possible to have:
BestAsk(YES) + BestAsk(NO) ≠ 1
It may even be greater than 1 or less than 1, creating arbitrage opportunities within the same market.
The basic elements of the order book:
Bid: Someone is willing to buy YES at this price.
Ask: Someone is willing to sell YES at this price.
Best Bid: The current highest buying price.
Best Ask: The current lowest selling price.
Depth: The quantity others have listed at each price level.
Your trading at the execution level is merely interacting with this order book. All actions can be categorized into four types:
1. Market Buy YES (Taker: Sweeping Ask)
You directly "consume" the current lowest selling price (Best Ask) and subsequent higher-priced sell orders.
Your average transaction price is actually a slippage function; simply put, the deeper you sweep, the more expensive the average price becomes.
2. Limit Buy YES (Maker: Placing Bid)
You place a buy order on the order book, specifying the highest price you are willing to pay.
You will only be executed if someone is willing to sell to you at that price.
Execution price = the price you placed.
You are acting as "the provider of liquidity."
3. Market Sell YES (Taker: Hitting Bid)
You directly sell your YES to the highest buy order (Best Bid).
Average execution price = the weighted average of the buy orders as you sell.
4. Limit Sell YES (Maker: Placing Ask)
You place a sell order on the order book, specifying the lowest price you are willing to sell.
You will only be executed if someone is willing to buy at that price (or higher).
You are also providing liquidity.
(The order book for NO-Token mirrors this and holds true similarly.)
The key point here is: Polymarket's "price" is not an automatically generated function but the result of real-time supply and demand interactions. Therefore, the order books for YES and NO can misalign in a short time frame. This is precisely where professional arbitrageurs will focus.
4.2 Valuation Layer: Fair Value = Risk-Neutral Probability = N(d2)
The order book tells us "at which price transactions occur," but it does not tell us "whether this price is reasonable."
When the prediction target is a financial asset (for example, "Will BTC be above $120,000 on December 31?"), the YES-Token on Polymarket is essentially a digital cash-or-nothing call option:
YES = "If (S_T > K) at expiration, pay $1; otherwise, pay $0."
NO = "If (S_T ≤ K) at expiration, pay $1; otherwise, pay $0."
In the classic Black–Scholes–Merton framework, the no-arbitrage pricing formula for such contracts is well-known:
- Risk-neutral price of the digital call (YES):
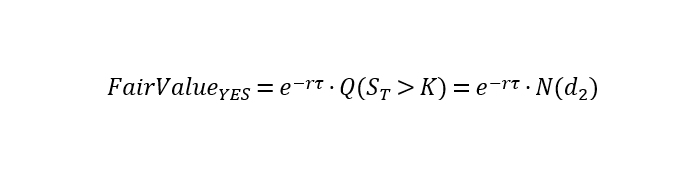
- Risk-neutral price of the digital put (NO):
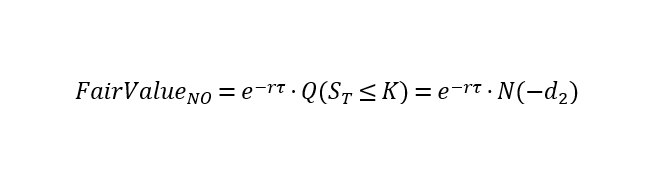
Where:
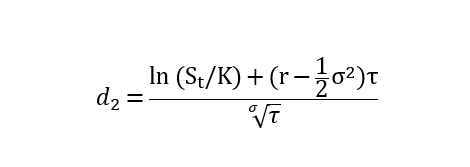
N(⋅) is the cumulative distribution function of the standard normal distribution.
τ = T - t is the remaining time to expiration (in years).
St_ is the current price of the underlying asset (e.g., current BTC price).
K is the "threshold price" (e.g., $120,000).
r is the risk-free interest rate (approximately available from the short-end dollar rate or stablecoin lending rate for the same term).
σ is the implied volatility (backed out from mature options markets like Deribit for similar expiration/strike prices).
What makes Polymarket unique is that it does not "pay at expiration," but rather "the 1 USDC collateral has already been locked in on Day 0." In other words, the discount factor e^(-rτ) in the traditional formula has already been structurally borne by the market maker/minting party.
For ordinary traders, this often means: V(YES) ≈ Q(ST > K) = N(d2)_
That is: the YES quote on Polymarket is close to "the probability that the underlying price exceeds K in a risk-neutral world."

How to use this in reality?
Obtain implied volatility σ from external options markets like Deribit.
Calculate N(d2).
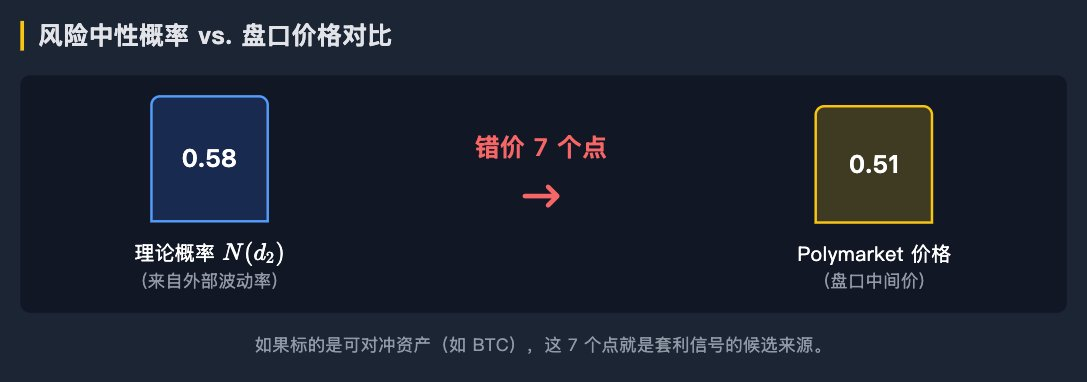
Compare N(d2) (theoretical fair value) with the mid-price of YES in the Polymarket order book: a) If Polymarket is significantly cheap: buying YES (or selling NO) may be a positive expectation; b) If Polymarket is significantly expensive: you can take the opposite action while hedging in the external market.
This is the Alpha that professional traders focus on:
CLOB trading prices vs. BSM risk-neutral probabilities.
5. Time Structure, Tail-End Behavior, and Role Switching
The derivation in the fourth part gives us a beautiful conclusion: "The price of Polymarket YES ≈ Risk-Neutral Probability (N(d2))," and we can use it to compare with mature options markets like Deribit to find mispricings.
However, there is a key complexity in the real world: The expiration settlement times of Polymarket and Deribit do not align perfectly.
Deribit offers standardized options with daily, weekly, monthly, quarterly, and annual expirations.
Polymarket's event markets can be extremely short (15 minutes, 1 hour, 4 hours) or can also be daily, weekly, monthly, quarterly, annually, or even "whether a specific state holds at a specific point in time."
Events with the same cycle also face risks of inconsistent settlement times.
This difference affects two of the most important things:
Can you perform "risk-free" cross-platform arbitrage?
What type of trader should you be on different time scales?
Next, we will formally break time into three categories: Short-term / Medium-term / Long-term, along with two key periods: Early Opening and Late Near Settlement. We will see that different intervals are actually playing completely different games.
5.1 Short-Term Markets (15 minutes / 1 hour / 4 hours)
Opening phase: Why is it often close to 0.50 / 0.50?
In ultra-short cycle markets (especially 15 minutes and 1 hour), you often see YES ≈ 0.50 and NO ≈ 0.50 appearing symmetrically right after opening. This does not mean "the market truly believes the probability is 50% vs 50%." Rather, it is because:
Inventory management priority > Probability expression.
At the moment the short-term market goes live, no one (especially market makers) is willing to immediately take on heavy unilateral risk. If YES is quoted at 0.80 right away, it essentially tells the market, "I am willing to take on a large amount of NO counterparty risk," which is too concentrated and too fast.Market makers prioritize symmetrical inventory over directional bets.
In other words, the early 0.50 / 0.50 is more like "please everyone place your orders, I will take a bit of inventory on both sides," rather than "objective probability = 50%."
"Short-term contracts at opening are often 'inventory-neutral quoting' rather than 'probability-neutral pricing.'"
Late Stage: Why is it said that "the late stage will be swept"? Is it manipulating probabilities?
As the settlement approaches (for example, in the last 1 minute/30 seconds), the real world often has already nearly determined the outcome:
- Example: With 30 seconds left until the deadline, if BTC is still clearly above the threshold, then YES is basically destined to redeem for $1. At this point, the real probability is close to 99%, which is almost indistinguishable from 1.
At this time, a very typical behavior occurs in the market:
There may still be people willing to sell YES at prices like 0.82 or 0.85, simply because they want to cash out immediately, not wanting to wait until the last second, and do not want to bear any tail risk;
At the same time, the market depth has usually become very shallow (market makers will withdraw depth in the late stage to avoid being crushed by the last-minute sell-off).
Active funds (large funds) will at this stage directly use a large market order to swallow these "cheap YES" in one go. The result is:
The screen price of YES will instantly jump to 0.95, 0.98, 0.99;
The screen price of NO will simultaneously be driven down to 0.05, 0.02, 0.01.
This does not mean "capital is manipulating probabilities." In fact, it is not. The core is:
They are not changing whether the event will happen (the real probability is almost already determined).
They are harvesting the chips that are still being sold at a discount, which are almost certain to redeem for $1, and consuming the "unclaimed certain profit" that has not yet been taken.
In other words, the large orders in the late stage are essentially "pushing the price close to the final redemption value while taking away the free money left on the table," rather than "changing the world's probability from 70% to 95%."
This is what is referred to as "locking in profits in the late stage / squeezing residual value."
This also explains why the risk in the late stage is more about the risk to those who want to close their positions early rather than the risk to those who will receive the final settlement:
If you are willing to hold your position until the final decision, then the probability is already on your side, and others cannot sweep away your final payout.
If you want to "close your position and cash out" in the last few seconds, then sorry, liquidity will be extremely one-sided, and your execution price may be squeezed by others.
Summary of the Short-Term Market:
Early: 0.50/0.50 is mainly for inventory management and does not represent the true probability.
Late stage: Prices instantaneously spike to 0.95+/0.05-, not manipulating the future, but sweeping away the last "unclaimed certain profit" on the table.
In this type of market, what role do you play? At the opening: inventory-type market maker (earning a spread, controlling exposure); in the late stage: liquidator vs. those wanting to exit (a liquidity battle, not an information battle).
5.2 Medium-Term Market ("Intraday / At a specific time today")
Medium-term contracts (for example, "Will BTC be above $120,000 before 20:00 today?" or "Will a certain vote pass tonight?") typically last from several hours to a day.
The difference between this type of market and ultra-short-term markets is:
The opening price is often no longer mechanically 0.50.
These questions often have a clear informational background (news, polls, on-chain data, order book structure), and early quotes can directly reflect market consensus, such as 0.65, 0.72, 0.30, rather than "placing 0.50 to balance inventory first." In other words, the opening may be "information-neutral pricing" (I quote based on expected probability) rather than "inventory-neutral pricing."Prices will deviate from 0.50 as information refreshes.
Any sudden developments on the day (regulatory statements, influencer leaks, voting counting progress) will be reflected in the price in real-time. This segment of the price is clearly expressing "how likely we think it is to happen."In the late stage, there is still the last 'spread squeeze.'
As the deadline approaches, if the event outcome is almost certain, active funds will still sweep YES to 0.95+ and drive NO down to 0.05-, for the same reasons as in the short-term market:
To consume the remaining chips that are still mispriced;
To make the last transaction price on the screen very close to the final 1 or 0;
Those wanting to close their positions will have to accept extremely unfavorable prices.
For the medium-term market, the role transition is:
Mid-stage: You are a "directional trader" (you are betting on opinions, news, information differences).
Late stage: You must switch to being a "position defender," and your task is to protect your already floating profits from being squeezed by late-stage liquidity, rather than naively acting as a public market maker.
5.3 Long-Term Market (Weekly / Monthly / Quarterly / Yearly)
The structure of long-term contracts (for example, "Will BTC be above $120,000 at the end of the quarter?" or "Will a certain policy take effect by the end of the year?") is completely different from the previous ones.
The opening price is usually far from 0.50, directly reflecting market priors.
There is no need to "start at 0.50 as a buffer" because: these events have often been institutionalized, researched, tracked by the media, and reflected in the derivatives market; and large participants at these time scales can hedge their exposure using external markets (futures, options, perpetual contracts) rather than going in naked. Therefore, the initial price of long-term events is often directly "our pricing expression of probability," such as 0.18, 0.73, 0.86, rather than politely starting from 0.50.Prices can connect with risk-neutral probabilities. For events linked to financial assets (for example, "Will BTC be above a certain threshold K at the end of the quarter?"), Polymarket's YES is like a cash-or-nothing digital call option:
If the event occurs, redeem for $1; if not, redeem for $0. In traditional options pricing, the theoretical price of such contracts is FairValue = e^(−rτ)⋅N(d2), which is "the present value of future $1 × risk-neutral probability." The difference with Polymarket is: the redemption funds are fully collateralized and locked in on Day 0, not collected from losers at expiration. This structurally pre-positions the part of the traditional formula that "discounts future $1 back." Traders often approximate Polymarket's YES price as: V(YES) ≈ Q(ST > K) = N(d2) — that is, the probability that "the underlying will be above the threshold at expiration" in a risk-neutral world. More practically:You can compare Polymarket's YES price with the implied probability curve (N(d_2)) from external options/futures markets like Deribit and ask:
"Who is selling a more expensive probability? Where is the mispricing of risk-neutral probability?" This is what professional funds do: cross-market relative value trading, buying "cheap probabilities" in one market and selling "expensive probabilities" in another, while using futures/options/perpetuals to hedge directional risk.
In the late stage of long-term contracts, it is not about "liquidity squeezing who runs first," but rather "settling probabilities close to 1 or 0."
These contracts often reach their final days/hours, and the probabilities themselves have already been locked in by macro realities (for example, BTC is far above/below the threshold, or a certain regulatory event has been publicly announced). The large orders in the late stage are more about aligning the remaining pricing to "almost 100%" or "almost 0%" rather than playing high-frequency harvesting to squeeze out 15-20 points in a few seconds.
In other words:
In the long-term market, the main focus is not on "late-stage firepower advantage," but rather "whose probability model is more reliable and whose cross-market hedging is cleaner."
5.4 Summary of the Three Types of Markets
Short-Term (15m / 1h / 4h)
The opening price is often around 0.50/0.50, aimed at balancing inventory, not because the probability is truly fifty-fifty.
The late stage is a liquidity clearing battle: active funds sweep away the "almost certain $1" that has not yet been taken, pushing the price to 0.95+/0.05-, squeezing the last profit.
Your identity: inventory-type market maker / late-stage risk mitigator.
Medium-Term (Intraday / At a specific time today)
The opening is not necessarily 0.50, as prior information already exists.
The in-market price expresses the market's subjective view on probability and jumps with news.
In the late stage, there will still be sweeping actions to lock in one-sided profits; you need to protect your floating profits rather than pretend to be a public liquidity pool.
Your identity: directional bettor in the mid-stage, position defender in the late stage.
Long-Term (Weekly / Monthly / Quarterly / Yearly)
The opening can be far from 0.50, as everyone can hedge and quantify probabilities.
YES becomes "almost a ticket to risk-neutral probability," which can be compared with the implied probabilities (N(d_2)) from external markets like Deribit for relative value trading.
The late stage resembles probabilities gradually converging to 1 or 0, rather than violent sweeps in the last 30 seconds to grab residual value.
Your identity: probability/volatility pricing agent, engaging in cross-market hedging rather than rushing the late stage.
6. Conclusion
We can now compress the pricing system of the prediction market Polymarket into a continuous link from mathematics to strategy:
1. Probability Axiom Layer: P(Yes) + P(No) = 1
——Any future event is primarily a sample space and probability measure problem.
2. Financial Engineering Layer (Fully Collateralized)
The market structurally guarantees that "winners can always redeem for $1" and forces V(Yes) + V(No) ≈ $1 through no-arbitrage pressure.
——This transforms abstract probabilities into a cash flow commitment that can be redeemed.
3. No-Arbitrage Pricing Layer
The fair price of YES equals its expected cash flow, which is the risk-neutral probability.
Under ideal conditions: V(Yes) ≈ Q(Yes)
4. Market Microstructure Layer (CLOB)
Actual transaction prices come from order book depth and slippage, rather than a static formula. The two order books for YES and NO may briefly misalign, which itself can create arbitrage opportunities.
5. Time Structure and Trading Role Layer
Short-term: Inventory game, preventing late-stage blow-ups.
Medium-term: Directional game + late-stage offense and defense.
Long-term: Probability game + cross-market relative value (Polymarket vs Deribit implied probabilities).
——Here, it is no longer a "single market price," but three completely different business models that shift with the time scale.

Risk Warning: The above analysis describes the structural pricing logic and no-arbitrage relationship, rather than specific investment advice. Actual trading must consider platform risk, oracle risk, regulatory risk, and capital occupation costs.
免责声明:本文章仅代表作者个人观点,不代表本平台的立场和观点。本文章仅供信息分享,不构成对任何人的任何投资建议。用户与作者之间的任何争议,与本平台无关。如网页中刊载的文章或图片涉及侵权,请提供相关的权利证明和身份证明发送邮件到support@aicoin.com,本平台相关工作人员将会进行核查。




